Unlock Top University Opportunities
See how much more graduates from these universities earn over their lifetime compared to the average graduate.
Cambridge
Average Graduate Salary
£75,000
80% higher than average UK graduate salary
Imperial
Average Graduate Salary
£72,000
80% higher than average UK graduate salary
LSE
Average Graduate Salary
£70,000
80% higher than average UK graduate salary
Why Choose Our Platform
We've helped hundreds of students secure places at top universities through our specialized TMUA preparation.
Our Platform
- ✓
Original TMUA-style questions
Created by Cambridge graduates who scored in the top 10% on the TMUA
- ✓
Detailed analytics
Track your progress and identify areas for improvement
- ✓
Timed mock tests
Simulate the real exam experience with our timed tests
- ✓
Comprehensive solutions
Step-by-step explanations for every question
Other Resources
- ✗
Generic math questions
Not specifically designed for the TMUA format or difficulty level
- ✗
Limited practice material
Only a handful of past papers available
- ✗
No personalized feedback
No way to track your progress or identify weaknesses
- ✗
Basic solutions
Minimal explanations without teaching the underlying concepts
Who We Are
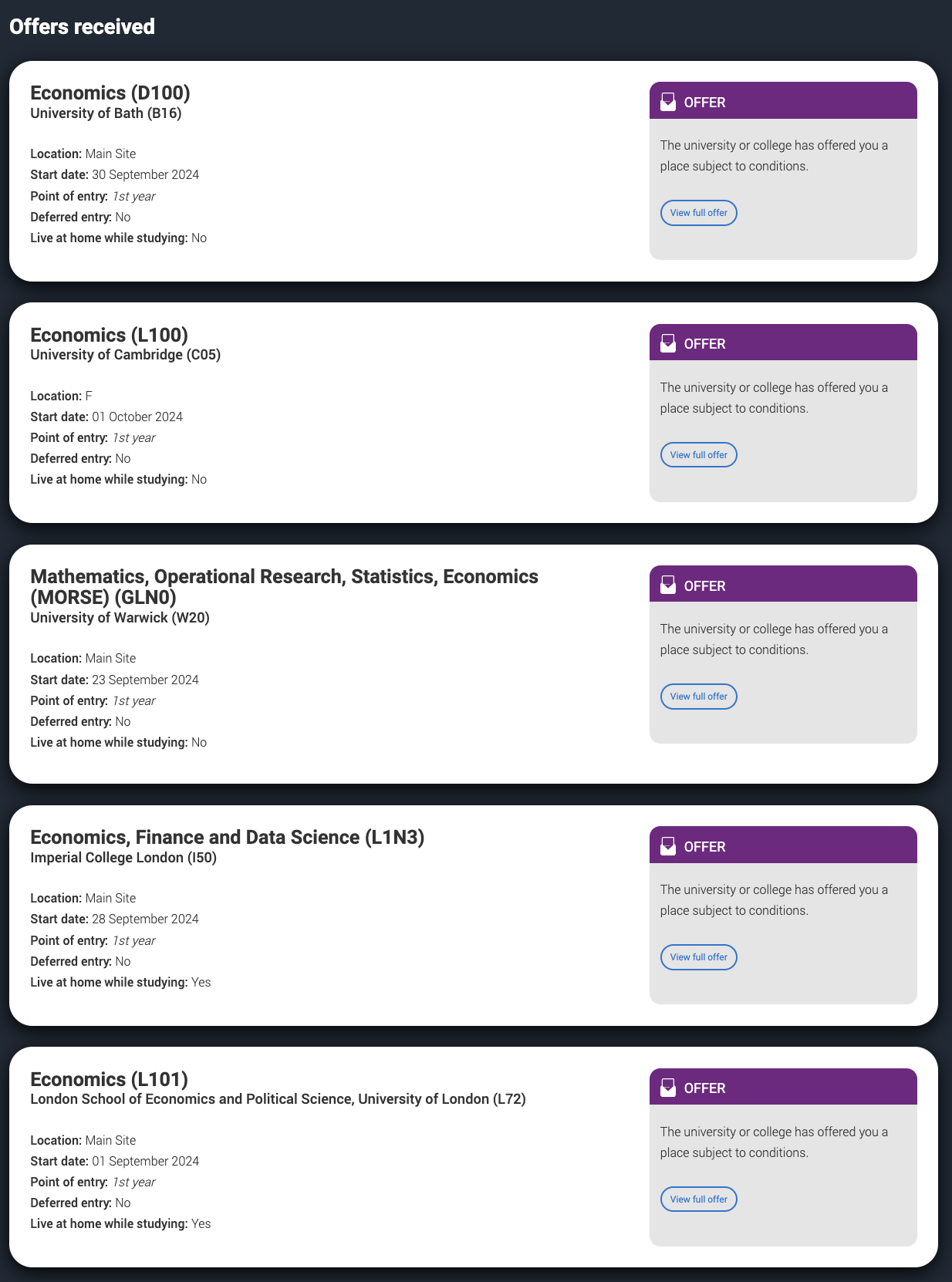
We're a team of TMUA experts dedicated to helping you succeed. Our founder, currently studying Economics at Cambridge, achieved 5/5 UCAS offers, including LSE Economics (1 in 11) and Imperial Economics, Finance, Data Science (1 in 15).
Our team also includes International Mathematical Olympiad participants and individuals with 8.0+ TMUA scores.
Our Success
Free TMUA Cheatsheet
Download our comprehensive TMUA cheatsheet covering all the key formulas and concepts you need to know for the exam.
What's Inside:
- ✓Essential formulas for Paper 1 & 2
- ✓Key concepts and definitions
- ✓Common question types and strategies
- ✓Time-saving techniques
- ✓Quick reference guide for exam day
Choose Your Package
Select the package that best fits your needs and start your journey to TMUA success.